一、代入排除法
代入排除是最直观快捷的行测解题方法。在两种情况下考虑用代入排除法:一是看到多位数问题、年龄问题、同余问题等题型,用代入排除;二是没有思路和方向的时候,考虑代入排除。
【例1】有四个学生恰好一个比一个大一岁,他们的年龄相乘等于93024,问其中最大的年龄是多少岁?( )
A.16岁B.18岁
C.19岁D.20岁
【答案】C
【解析】直接求解比较麻烦,考虑代入排除。带入A选项,最大的16岁,这几个人就是16,15,14,13。四个数的乘积尾数为0,不符合,排除。同理排除BD。因此答案选择C选项。
二、数字特性法
【例1】(2008-广东-15)某年级有4个班,不算甲班其余三个班的总人数是131人;不算丁班其余三个班的总人数是134人;乙、丙两班的总人数比甲、丁两班的总人数少1人,问这四个班共有多少人?
A.177 B.176
C.266 D.265
【答案】A
【解析】考虑数字特性法中的奇偶特性。乙、丙两班总人数比甲、丁两班总人数少1人,运用奇偶特性可知乙、丙与甲、丁之和也就是四个班总人数必然是奇数,排除B、C。由题意(乙+丙+丁)+(甲+乙+丙)=131+134=265,可以推出四个班人数小于265,因此答案选择A选项。
三、比例法
比例是各数或各物理量之间的对比关系。凡是符合等式A=M×N的形式,其中,A、M、N代表不同的物理量,且三个量中必须有一个量确定,都可以采用比例法。在实际的应用中,诸如路程=速度×时间,收入=单价×销量等均符合条件。当A固定时,M与N成反比例关系;当M固定时,A与N成正比例关系。
【2012浙江-53】A、B两地间有条公路,甲乙两人分别从A、B两地出发相向而行,甲先走半小时后,乙才出发,一小时后两人相遇,甲的速度是乙的2/3。问甲、乙所走的路程之比是多少?
A.5:6B.1:1
C.6:5D.4:3
【答案】B
【解析】本题考核行程问题。路程=速度×时间。V甲:V乙=2:3,T甲:T乙=1.5:1,则S甲:S乙=2×1.5:3×1=1:1。因此,答案选择B选项。
【2008年山东-43】两个相同的瓶子装满酒精溶液,一个瓶子中酒精与水的体积比是 3:1,另一个瓶子中酒精与水的体积比是 4:1,若把两瓶酒精溶液混合,则混合后的酒精和水的体积之比是多少?
A.31:9B.7:2
C.31:40D.20:11
【答案】A
【解析】本题考核溶液问题。两个瓶子体积相同,酒精和水的体积比分别为“3:1”和“4:1”,分别将瓶子分成“3+1=4”和“4+1=5”份,因此,要变成“和同”的比例形式。4和5的最小公倍数为20,则3:1=15:5,4:1=16:4,混合后酒精和水的体积比=(15+16):(5+4)=31:9。因此,答案选择A选项。
四、赋值法
【例1】(国考2012-71)2010年某种货物的进口价格是15元/公斤,2011年该货物的进口量增加了一半,进口金额增加了20%。问2011年该货物的进口价格是多少元/公斤?
A.10 B.12 C.18 D.24
【答案】 B
【解析】题中2010与2011两年中的进口价、进口量和进口金额发生改变,故可赋值2010年的进口量为2公斤,则2011年的进口量为3公斤,两年中单价、数量和金额的数量关系如下图所示:
| 年 份 | 进口价格(元/公斤) | 进口量(公斤) | 进口金额(元) |
| 2010年 | 15 | 2 | 30 |
| 2011年 | 12 | 3 | 36 |
2010年进口额=15×2=30 元,则2011年进口额=30×(1+20%)=36元,那么2011年的进口价格=36÷3=12元 故2011年该货物的进口价格是12元/公斤。因此答案选择B选项。

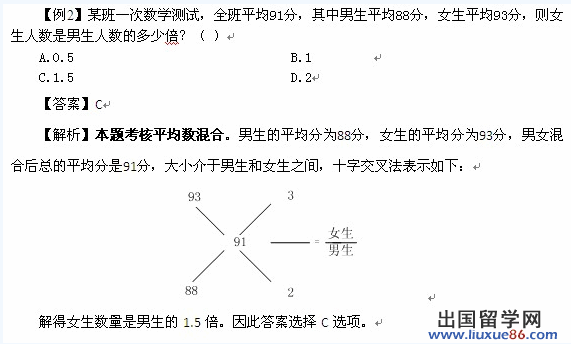
五、十字交叉法
十字交叉法在溶液问题、经济问题、工程问题和和差倍比问题中均有着广泛的应用。
【例1】(2010贵州-9)要将浓度分别为20%和5%的A、B两种食盐水混合配成浓度为15%的食盐水900克。问5%的食盐水需要多少克?( )
A.250B.285
C.300D.325
【答案】C.

| 行测真题 | 行测答案 | 行测答题技巧 | 行测题库 | 模拟试题 |

