任何一场考试取得成功都离不开每日点点滴滴的积累,下面由留学群小编为你精心准备了“行测数量关系技巧:如何解决植树问题”,持续关注本站将可以持续获取更多的考试资讯!
行测数量关系技巧:如何解决植树问题
植树问题,在行测考试中属于常见计算问题中一种。这一类题型相对比较简单,但是每年的得分率较低。究其原因,很多人在阅读题干时,常常因为文字描述的不同,误入“陷阱”,没有注意到其中一些小细节。如何避免粗心大意,和小编一起来学习一下。
一、非封闭区域植树问题
【例1】有一条堤全长 500 米,从头到尾每隔 5 米种植白杨树一棵,一共可以种( )棵。
A.100 B.101 C.99 D.102
【易错项】选A,500÷5=100棵
【正确答案】选B,从头到尾植树,意味着两端必须有树,500÷5=100棵,是除去第一棵以外的其他树,还需把第一棵树也算在内,500÷5+1=101棵。
【例2】有一条新修的道路,现在需要在该道路的两边植树,已知路长为 5052 米,如果道路两端植树且每两棵树间隔 6 米,那么一共需要植多少棵树?
A.842 B.843 C.1686 D.1628
【易错项】选B,5052÷6+1=843棵
【正确答案】选C,除了有道路两端植树的要求,还有道路两边,算完一侧的棵数后,一共需要植树 2×(5052÷6+1)=1686 棵。
二、封闭区域植树问题
【例3】在一周长为 50m 的花坛周围种树,如果每隔 5m 种一棵,共要种多少棵树?
A.9 B.10 C.11 D.12
【易错项】选C,50÷5+1=11棵
【正确答案】选B。此题为封闭路线种树问题,与封闭区域不同,不用计算再考虑第一棵树,首尾相连只算一次即可,树的数量=周长÷间隔长度,共要种树 50÷5=10 棵。
三、植树问题升级篇
【例4】一小圆形场地的半径为 100 米,在其边缘均匀种植 200 棵树木,然后又在其任两条直径上,每隔 2 米栽种一棵树木。问最少要种植多少棵树木?
A.397 B.398 C.399 D.400
【易错项】选B,(200÷2+1-2)×2=398棵
【正确答案】选A。每条直径上种 200÷2+1=101 棵树,直径两端的树与边缘的树重
合时棵数最少,且两条直径的圆心所种树必然重合,共 200+101×2-2×2-1=397 棵。
四、如何解决植树问题的小窍门
非封闭区域植树:
1.若两端都种植,则种植棵树=间距数+1;
2.若两端不种植,则种植棵树=间距数-1;
3.若一端种植一端不种植,则种植棵树=间距数。
封闭区域植树:
种植棵树=间距数(也就等于非封闭区域一端种植一端不种植)。
行测技巧:一道题多种解法,方法知识一起学
几何问题是行测考试常见的考点之一,小编通过深入剖析,让大家了解这道题的多种解法,拓展思路,同时考生们也能学习一些几何基本知识点,一举两得。
例题:将一块长10厘米、宽4厘米的长方形平板切割成A、B、C共3块,其中C块的面积为22平方厘米,B为等腰三角形,那么A块的面积是( )。
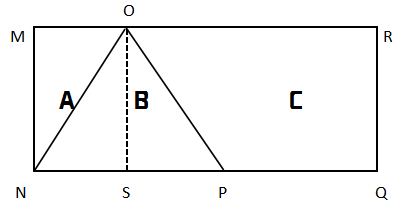
A.6平方厘米 B.12平方厘米 C.8平方厘米 D.4平方厘米
一、巧用两种图形的基本性质
本题给出一个条件,即B是一个等腰直角三角形,等腰三角形有几个基本性质,想必大家都比较熟悉,比如两条腰相等;从两腰之间的顶点往底边作垂线,那此线就是三线合一,即垂直于底边、平分顶角、平分底边。如上图,从O点做垂线OS,这条线把是三角形B分成两个一样的三角形,当然这两个三角形的面积肯定是相等的,在观察四边形MNSO构成一个长方形,而ON正好是长方形的对角线,根据长方形的基本性质,对角线所分的两个三角形大小相等,所以面积也相等,综上可知,以上三个图中左边的三个三角形面积都相等,而已知大长方形面积为10×4=40,且C区域面积是22,所以剩下的三个三角形的区域是40-22=18,18÷3=6即是所求的三角形的面积。
这种方法费时最少,技巧性比较强。用到的几何知识点有:等腰三角形“三线合一”的基本性质,长方形的对角线的性质,长方形的面积公式等知识点。
二、巧用三角形全等和方程法
第二种方法相较于第一种方法计算的过程要相对复杂,但也是考生们的正常思考路径。 从P点向RM边作垂线。利用三角形NOP是等腰三角形的性质,可以证明三角形OMN和三角形OSP全等。怎么证明呢,已知这两个三角形都是直角三角形,我们知道直角三角形有一个特殊的证明方法,简称“HL”,“H”是直角边;在本题中指的是MN=SP,“L”是斜边,指的是ON=OP。
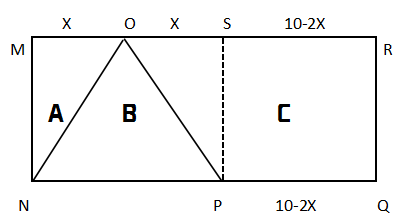
证明全等后,可以得到OM=OS。已知C区域是面积是22,C还是一个梯形。梯形的面积公式是:(上底+下底)×高÷2,可以设未知线段OS=OM为X,可以得到梯形的较长的底边长为10-X,而SPQR构成的是一个矩形,那SR=PQ=10-2X,PQ即为梯形较短的底边。高已知是RQ=4,可列方程:(10-2X+10-X)×4÷2=22,解得X=3。那三角形A的面积就是4×3÷2=6。
本题所用到的知识点除了梯形的面积公式以外,还有:三角形全等的证明和边长相等的性质、矩形对应边相等的性质。
三、巧用方程组和梯形公式

本题为了利用梯形公式,还可用方程的方法去做。
OR和PQ都是未知条件,分别设为X和Y,那OM=10-X,NS=SP=10-X,PQ=10-2×(10-X)=Y,化简可得方程:2X-Y=10,又已知梯形面积为:(X+Y)×4÷2=22,化简得X+Y=11,联立两个方程为方程组,解得x=7,OM=10-X=10-7=3,计算可得三角形A的面积为6。
此解法与以上两种解法所用知识点部分重复,不再一一列举。
推荐阅读:
| 行测真题 | 行测答案 | 行测答题技巧 | 行测题库 | 模拟试题 |

