我在想什么是天才?天才就是努力勤奋的结果。只要肯努力,梦想总会实现。 下面是留学群为大家编辑整理的“2022年高考数学(理)模拟卷(全国卷)二轮拔高卷01”此文本仅供参考,欢迎阅读。
![]() 2022年高考数学(理)模拟卷(全国卷)
2022年高考数学(理)模拟卷(全国卷)
二轮拔高卷01
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合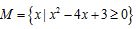 ,
,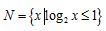 ,则集合
,则集合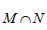 =( )
=( )
A.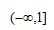 B.
B.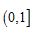 C.
C. 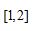 D.
D.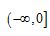
2.已知i为虚数单位,则复数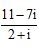 在复平面内对应的点在( )
在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
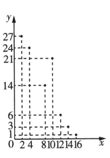
3.相关变量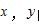 的散点图如图所示,现对这两个变量进行线性相关分析,方案一:根据图中所有数据,得到回归直线方程
的散点图如图所示,现对这两个变量进行线性相关分析,方案一:根据图中所有数据,得到回归直线方程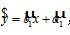 ,相关系数为
,相关系数为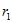 ;方案二:剔除点
;方案二:剔除点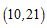 ,根据剩下的数据得到回归直线方程,相关系数为
,根据剩下的数据得到回归直线方程,相关系数为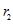 .则( )
.则( )
A.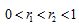 B.
B.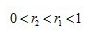
C.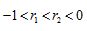 D.
D.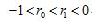
4.己知各项均为正数的等比数列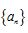 的前3项和为14,
的前3项和为14,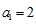 ,则数列
,则数列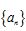 的公比等于( )
的公比等于( )
A.4 B. 3 C.2 D.1
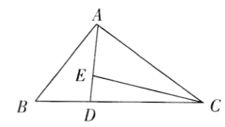
5.如图,在口ABC中,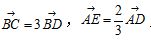 ,则
,则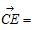 ( )
( )
A.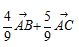 B.
B.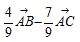 C.
C.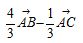 D.
D.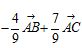
6.已知函数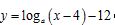 (
(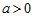 且
且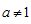 )的图象过定点P,且角
)的图象过定点P,且角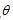 的终边经过P,则
的终边经过P,则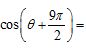 ( )
( )
A.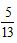 B.
B.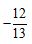 C.
C.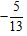 D.
D.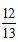
7.已知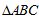 中,
中,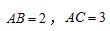 ,且
,且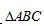 的面积为
的面积为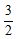 ,则
,则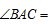 ( )
( )
A.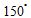 B.
B.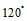 C.
C.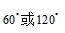 D.
D.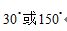
8.抛物线有如下光学性质:平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点.已知抛物线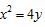 的焦点为F,一条平行于y轴的光线从点
的焦点为F,一条平行于y轴的光线从点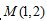 射出,经过抛物线上的点A反射后,再经抛物线上的另一点B射出,则经点B反射后的反射光线必过点( )
射出,经过抛物线上的点A反射后,再经抛物线上的另一点B射出,则经点B反射后的反射光线必过点( )
A.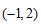 B.
B.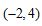 C.
C.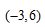 D.
D.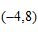
9.在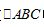 中,M为边BC上的点,且
中,M为边BC上的点,且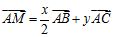 ,满足则
,满足则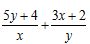 ( )
( )
A.有最小值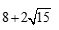 B.有最小值
B.有最小值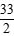
C.有最小值12 D.有最小值16
10.北京时间2021年10月16日0时23分,搭载神州十三号载人飞船的长征二号遥十三运载火箭,在酒泉卫星发射中心按照预定时间精准点火发射,约582秒后,神州十三号载人飞船与火箭成功分离,进入预定轨道,顺利将翟志刚、王亚平、叶光富3名航天员送入太空,发射取得圆满成功.据测算:在不考虑空气阻力的条件下,火箭的最大速度V(单位:m/s)和燃料的质量M(单位:kg)、火箭的质量(除燃料外)m(单位:kg)的函数关系是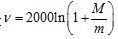 .当火箭的最大速度达到11.5kg/s时,则燃料质量与火箭质量之比约为( )(参考数据:
.当火箭的最大速度达到11.5kg/s时,则燃料质量与火箭质量之比约为( )(参考数据: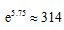 )
)

A.314 B.313 C.312 D.311
11.直线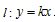 与双曲线
与双曲线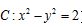 交于不同的两点,则斜率k的取值范围是( )
交于不同的两点,则斜率k的取值范围是( )
A.(0,1) B.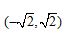 C.
C.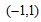 D.
D.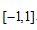
12.正四面体ABCD的棱长为4,E为棱AB的中点,过E作此正四面体的外接球的截面,则该截面面积的取值范围是( )
A.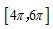 B.
B.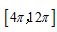
C.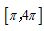 D.
D.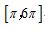
二、填空题:本题共4小题,每小题5分,共20分。
13.已知实数x,y满足不等式组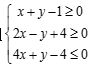 ,则
,则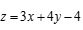 的最大值为________.
的最大值为________.
14.有4名男生和2名女生共6人组成两个志愿者队伍去两个不同的场馆,要求每队既有男生又有女生,则不同的分配方法有_______________种.(用数字表示)
15.已知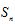 是
是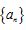 的前n项和,
的前n项和,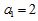 ,
,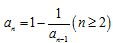 ,则
,则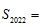 ______.
______.
16.已知函数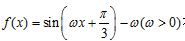 在区间
在区间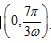 上有且仅有4个零点,则
上有且仅有4个零点,则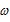 的取值范围是__________.
的取值范围是__________.
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)大学生是国家的未来,代表着国家可持续发展的实力,能够促进国家综合实力的提高.据统计,2016年至2020年我国高校毕业生人数y(单位:万人)的数据如下表:
年份 | 2016 | 2017 | 2018 | 2019 | 2020 |
年份代号x | 16 | 17 | 18 | 19 | 20 |
高校毕业生人数y(单位:万人) | 765 | 795 | 820 | 834 | 874 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性的强弱.
(已知: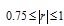 ,则认为y与x线性相关性很强;
,则认为y与x线性相关性很强;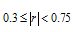 ,则认为y与x线性相关性一般;
,则认为y与x线性相关性一般;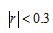 ,则认为y与x线性相关性较弱)
,则认为y与x线性相关性较弱)
(2)求y关于x的线性回归方程,并预测2022年我国高校毕业生的人数(结果取整数).
参考公式和数据: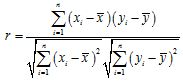 ,
,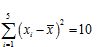 ,
,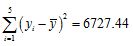 ,
,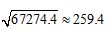 ,
,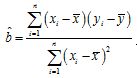 ,
,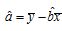 .
.
18.(12分)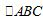 的内角A,B,C所对的边分别为a,b,c.已知
的内角A,B,C所对的边分别为a,b,c.已知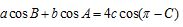 .
.
(1)求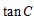 ;
;
(2)若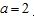 ,
,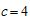 ,求
,求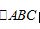 的周长.
的周长.
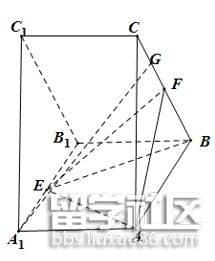
19.(12分)如图,在三棱柱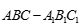 中,侧面
中,侧面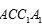 是矩形,
是矩形,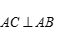 ,
,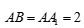 ,
,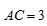 ,
,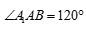 ,E,F分别为棱
,E,F分别为棱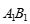 ,BC的中点,G为线段CF的中点.
,BC的中点,G为线段CF的中点.
(1)证明: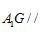 平面
平面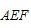 ;
;
(2)求二面角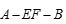 的余弦值.
的余弦值.
20.(12分)已知定圆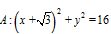 ,圆心为A;动圆M过点
,圆心为A;动圆M过点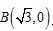 且与圆A相切,圆心M的坐标为
且与圆A相切,圆心M的坐标为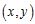 ,且
,且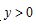 ,它的轨迹记为C
,它的轨迹记为C
(1)求曲线C的方程;
(2)过一点N(1,0)作两条互相垂直的直线与曲线C分别交于点p和Q,试问这两条直线能否使得向量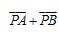 与
与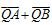 互相垂直?若存在,求出点
互相垂直?若存在,求出点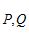 的横坐标,若不存在,请说明理由
的横坐标,若不存在,请说明理由
21.(12分)已知函数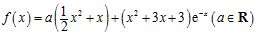 .
.
(1)当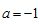 时,求曲线
时,求曲线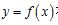 在点(0,f(0))处的切线方程;
在点(0,f(0))处的切线方程;
(2)若函数f(x)有三个极值点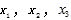 ,且
,且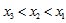 .证明:
.证明: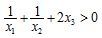 .
.
(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
22.[选修4-4:坐标系与参数方程](10分)
已知直线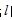 的方程为
的方程为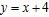 ,圆C的参数方程为
,圆C的参数方程为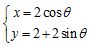 (
(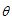 为参数),以原点为极点,
为参数),以原点为极点,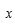 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求直线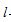 与圆C的交点的极坐标;
与圆C的交点的极坐标;
(2)若P为圆C上的动点,求P到直线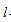 的距离d的最大值.
的距离d的最大值.
23.[选修4-5:不等式选讲](10分)
已知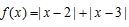 .
.
(1)解不等式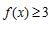 ;
;
(2)记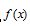 的最小值为
的最小值为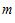 ,若a,b都是正数,且
,若a,b都是正数,且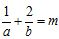 ,证明:
,证明: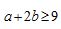 .
.
| 高考语文复习资料 | 高考数学复习资料 | 高考英语复习资料 | 高考文综复习资料 | 高考理综复习资料 |
| 高考语文模拟试题 | 高考数学模拟试题 | 高考英语模拟试题 | 高考文综模拟试题 | 高考理综模拟试题 |
| 高中学习方法 | 高考复习方法 | 高考状元学习方法 | 高考饮食攻略 | 高考励志名言 |

