角的平分线的性质、判定
性质:在角的平分线上的点到这个角的两边的距离相等.
判定:到一个角的两边的距离相同的点,在这个角的平分线上.
等腰三角形的性质
1.等腰三角形的性质定理 等腰三角形的两个底角相等 (即等边对等角).
2.推论1 等腰三角形顶角的平分线平分底边并且垂直于底边 .
3.等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合.
4.推论3 等边三角形的各角都相等,并且每一个角都等于60° .
等腰三角形判定
1等腰三角形的判定定理 如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)
2.三个角都相等的三角形是等边三角形.
3.有一个角等于60°的等腰三角形是等边三角形.
线段垂直平分线的性质、判定
1. 定理: 线段垂直平分线上的点和这条线段两个端点的距离相等 .
2.逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
3.线段的垂直平分线可看作和线段两端点距离相等的所有点的集合
.
轴对称、中心对称、 平移、旋转
1. 关于某条直线对称的两个图形是全等形
2.如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线
3.两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上
4.若两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称.
5.关于中心对称的两个图形是全等的.
关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分.
6. 若两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点成中心对称.
7.平移或旋转前后的图形是不变的.中心对称是旋转的特殊形式。
勾股定理 直角三角形两直角边a、b的平方和、等于斜边c的平方,即a2+b2=c2 .
勾股定理的逆定理 如果三角形的三边长a、b、c有关系a2+b2=c2 ,那么这个三角形是直角①直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半.
②直角三角形斜边上的中线等于斜边上的一半.
n边形、四边形的内角和、外角和
1.四边形的内角和等于360°.
2.四边形的外角和等于360°
3.多边形内角和定理
n边形的内角的和等于(n-2)180°.
4.推论 任意多边的外角和等于360°.
平行四边形性质
1.平行四边形的对角相等.
2.平行四边形的对边相等.
3.夹在两条平行线间的平行线段相等.
4.平行四边形的对角线互相平分.
平行四边形判定
1.两组对边分别平行的四边形是平行四边形.
2.两组对角分别相等的四边形是平行四边形. 3.两组对边分别相等的四边形是平行四边形.
4.对角线互相平分的四边形是平行四边形.
5. 一组对边平行相等的四边形是平行四边形
矩形性质
1. 矩形的四个角都是直角 .
2. 矩形的对角线相等.
矩形判定
1.有一个角是直角的平行四边形是矩形.
2.有三个角是直角的四边形是矩形.
3. 对角线相等的平行四边形是矩形 .
菱形性质
1、菱形的四条边都相等.
2. 菱形的对角线互相垂直,并且每一条对角线平分一组对角.
3、菱形面积=对角线乘积的一半,即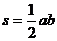
菱形判定
1.有一组邻边相等的平行四边形是菱形
2.四边都相等的四边形是菱形
3.对角线互相垂直的平行四边形是菱形.
正方形性质
1.正方形的四个角都是直角,四条边都相等.
2.正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角.
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |

