报考了初中教室资格考试面试的考生注意！小编整理出了关于初中面试的数学的试讲真题，详细的试讲真题已放在下文了，感兴趣的来看看吧！下面是留学群整理的“初中教师资格考试面试数学试讲真题”，此文本仅供参考，欢迎阅读。
初中数学
不等式的解集
一、【教学目标】
1.知识与技能：学生通过学习了解什么叫做不等式以及什么是不等式的解，掌握什么是不等式的解集以及求解的过程叫什么。
2.过程与方法：学生通过自主探究、小组合作等方式，经历解不等式的过程，提高了抽象思维的能力。
3.情感态度与价值观：学生通过本节课的学习，提高自主探究能力和抽象思维，体会数学的应用价值以及感受到数学来源于生活应用于生活。
二、【教学重难点】
1.教学重点：掌握不等式的概念以及不等式的解，解集的概念。
2.教学难点：理解不等式的解集，会在数轴上表示不等式的解。
三、【教学过程】
环节一：导入新课
【教师活动】多媒体导入，教师展示图片，询问学生从中可以得到哪些信息？
【学生活动】学生回答：两家商场推出不同的优惠方案，几个人在核算到哪家商场购物花费少？
【教师活动】提问：这个图片中蕴含的数学信息是什么？
【学生活动】蕴含了数学中不等的关系。
【教师活动】对于这样的问题，我们常常要把比较的对象数量化，分析其中的不等关系，列出相应的数学式子，通过解不等式而得出结论。
【教师活动】引入课题，不等式的解集。
【设计意图】通过实际生活情景导入，引发学生思考，提出问题，让学生产生求知欲，进而为本节课的学习打下了坚实的基础。
环节二：新课讲授
【教师活动】多媒体导入，展示课本问题。
【教师活动】询问学生车速应该满足什么条件？
【学生活动】学生分析，从时间上看，汽车要在12：00之前驶过A地，行驶的速度行驶50km所用的时间不到三分之二小时。
【教师活动】继续询问，我们可以得到怎么样的关系？
【学生活动】回答：可以设车速为xkm/h，即
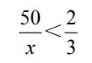
【教师活动】还可以怎么理解？
【学生活动】从路程上看，汽车要在12：00之前驶过A地，车速行驶三分之二小时的路程要超过50km。
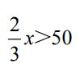
【教师活动】总结：像第一个式子和第二个式子用符号“＞”或“＜”表示大小关系的式子叫做不等式。
【教师活动】强调，有些不等式中含有未知数，有些不等式中不含未知数，例如“3＞2”等。
【教师活动】继续询问以上含有未知数的不等式，车速x应该满足什么条件，应该取哪些值？
【学生活动】回答：x=80，x=78，时，第二个不等式都满足条件，x=72，x=75时，不满足条件。
【学生活动】也就是当x取一些值时，不等式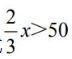
会成立，一些值不等式
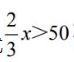不成立。
【教师活动】总结：与方程的解类似，我们把使不等式成立的未知数的值叫做不等式的解。例如80和78是不等式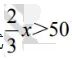
的解，75和72不是不等式
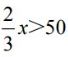的解。
【教师活动】询问除了以上数字满足条件，还有没有其他的数字满足条件？小组探究后汇报结果。
【学生活动】回答相关结论。例如x＞75时，不等式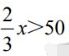
总成立，x＜75或者x=75不等式
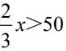不成立。
【教师活动】总结相关结论。
【教师活动】像这样的解集还可以表示在数轴上。（板书数轴）
【教师活动】由此可见，汽车要在12：00之前驶过A地，行驶速度必须超过75km/h。
【教师活动】总结：一般的，一个含有未知数的不等式的所有的解，组成这个不等式的解集。求解不等式的过程叫做解不等式。
环节三：巩固提高
表示并计算a的4倍大于8
环节四：小结作业
1.询问学生通过本节课的学习你有哪些收获？
2.作业布置：课后练习1-2题做到书上。
四、【板书设计】
五、【教学反思】
初中数学
一元二次方程根与系数的关系
一、教学目标
知识与技能：理解并掌握一元二次方程根与系数的关系，并能够运用该性质求解一元二次方程根的相关问题。
过程与方法：学生通过小组讨论、自主探究等过程，培养学生的创新意识和探究能力。
情感态度与价值观：通过情境教学过程，激发学生的求知欲望，培养学生积极学习数学的态度，增强解决问题的信心，获得解决问题的成功体验。
二、教学重难点
重点：一元二次方程根与系数的关系——韦达定理。
难点：方程中两个根之间关系的归纳探究过程。
三、教学过程
（一）导入新课
【教师活动】通过复习导入的形式询问学生有关一元二次方程的一般形式是怎样的？求根公式是什么？
【学生活动】学生通过思考很容易得出一元二次方程的一般形式和求根公式
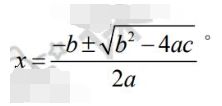
【教师活动】顺势提出问题“对于一元二次方程如果有2个根，那么这两个根在数值上是否存在某种特殊的关系呢”？进而导入新课。
【设计意图】复习原有的一元二次方程的求根公式，为接下来研究根与系数的关系，奠定了知识基础，有利于新课的探究。
（二）新课讲授
1.感知新知
【教师活动】教师出示一元二次方程
组织学生求解，猜想这两个根在数值上与方程的各项的系数有什么关系”
【学生活动】独立求解，得到方程的两个根。
【设计意图】通过一个简单的例子，学生可以先感知，两个根与系数的关系，提高数学抽象能力。
2.生成新知
【教师活动】引导学生将
进行展开，然后合并同类项，学生通过化简从而得到
【教师活动】引导学生用——p表示
并结合之前学习的有关一元二次方程的求根公式通过小组讨论探究两个根与一元二次方程的系数之间的关系。
【学生活动】学生通过小组讨论最终不难发现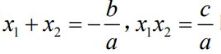
即韦达定理。
【设计意图】经历特殊到一般的腿到过程，发展学生的合情推理能力。
（三）巩固提高
1.让学生根据今天的所学知识完成课本例题
1：给出两个一元二次方程
并且引导学生根据韦达定理判断两个根的关系。帮助学生进一步巩固所学知识。
2.教师在学生解题过程中进行巡视，根据学生解题情况，提问学生解题思路以及运算结果。
3.教师根据学生的回答进行简单评价和总结。
（四）小结作业
1.询问学生通过本节课的学习你有哪些收获？
2.对学生的总结进行简单评价。
3.作业布置：根据课后练习题内容，考虑到不同层次学生的需求，设置必做题和选做题。
四、板书设计
推荐阅读：
| 教师资格证题库 | 教师考试备考辅导 | 教育学资料 | 教育心理学资料 | 综合素质资料 | 教育知识与能力 |