勾股定理
【课标要求】
|
考点
|
课标要求
|
知识与技能目标
|
|||
|
了解
|
理解
|
掌握
|
灵活应用
|
||
|
运用勾股定理及其逆定理解决简单问题
|
|
|
∨
|
∨
|
|
【知识梳理】
体验勾股定理的探索过程，会运用勾股定理解决简单问题；会用勾股定理的逆定理判定直角三角形。
【能力训练】
一、选择题
1.下列各数组中，不能作为直角三角形三边长的是 ( )
A. 9,12,15 B. 7,24,25 C. 6,8,10 D. 3,5,7
2.将直角三角形的各边都缩小或扩大同样的倍数后，得到的三角形 ( )
A. 可能是锐角三角形 B. 不可能是直角三角形
C. 仍然是直角三角形 D. 可能是钝角三角形
3.在测量旗杆的方案中，若旗杆高为21m，目测点到杆的距离为15m，则目测点到杆顶的距离为（设目高为1m） ( )
A.20m B.25m C.30m D.35m
4.一等腰三角形底边长为10cm，腰长为13cm，则腰上的高为 ( )
A. 12cm B.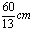 
C.
D.
C. D.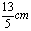 二、填空题
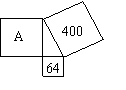
5.如图,64、400分别为所在正方形的面积，则图中字母A所代表的正方形面积是 _________ .
6.直角三角形两条直角边的长分别为5、12，则斜边上的高为 .
7.已知甲往东走了4km，乙往南走了3km，这时甲、乙两人相距 .
8.一个长方形的长为12cm，对角线长为13cm，则该长方形的周长为 .
9.以直角三角形的三边为边向形外作正方形P、Q、K，若SP＝4，SQ＝9，则Sk＝ .
三、解答题
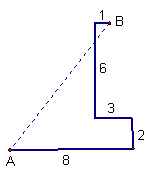
10.假期中，小明和同学们到某海岛上去探宝旅游，按照探宝图，他们登陆后先往东走8千米，又往北走2千米，遇到障碍后又往西走了3千米，再折向北走了6千米处往东一拐，仅走了1千米就找到宝藏，问登陆点A到宝藏埋藏点B的距离是多少千米？
11.P为正方形ABCD内一点，将△ABP绕B顺时针旋转90°到△CBE的位置，若BP＝a.求：以PE为边长的正方形的面积.
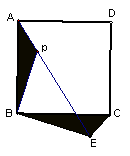
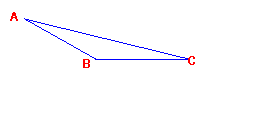
12.已知:如图13,△ABC中,AB=10,BC=9,AC=17. 求BC边上的高.
13.拼图填空：剪裁出若干个大小、形状完全相同的直角三角形，三边长分别记为a、b、c，如图①.（1）拼图一：分别用4张直角三角形纸片，拼成如图②③的形状，观察图②③可发现，图②中两个小正方形的面积之和__________ （填“大于”、“小于”或“等于”）图③中小正方形的面积，用关系式表示为________ .（2）拼图二：用4张直角三角形纸片拼成如图④的形状，观察图形可以发现，图中共有__________个正方形，它们的面积之间的关系是________ ，用关系式表示为_____ .（3）拼图三：用8个直角三角形纸片拼成如图⑤的形状，图中3个正方形的面积之间的关系是_____ _____ ，用关系式表示________ _______ .
参考答案：
一、选择题：1-4：DCBA
二、填空题：5．336；6．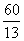
；7．5；8．34；9．5或13
；7．5；8．34；9．5或13 三、解答题：10．10Km；11．2a2；12．6；13．等于，其证明方案即为勾股定理的证明，最后的结论就是勾股定理。
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |