4.溶液(混合物)问题
溶液(混合物)问题有四个基本量:溶质(纯净物)、溶剂(杂质)、溶液(混合物)、浓度(含量)。其关系式为:①溶液=溶质+溶剂(混合物=纯净物+杂质);②浓度= ×100%=
×100%= ×100%【纯度(含量)=
×100%【纯度(含量)= ×100%=
×100%=
例11.把1000克浓度为80%的酒精配成浓度为60%的酒精,某同学未经考虑先加了300克水。⑴试通过计算说明该同学加水是否过量?⑵如果加水不过量,则应加入浓度为20%的酒精多少克?如果加水过量,则需再加入浓度为95%的酒精多少克?
讲评:溶液问题中浓度的变化有稀释(通过加溶剂或浓度低的溶液,将浓度高的溶液的浓度降低)、浓化(通过蒸发溶剂、加溶质、加浓度高的溶液,将低浓度溶液的浓度提高)两种情况。在浓度变化过程中主要要抓住溶质、溶剂两个关键量,并结合有关公式进行分析,就不难找到相等关系,从而列出方程。
本题中,⑴加水前,原溶液1000克,浓度为80%,溶质(纯酒精)为1000×80%克;设加x克水后,浓度为60%,此时溶液变为(1000+x)克,则溶质(纯酒精)为(1000+x)×60%克。由加水前后溶质未变,有(1000+x)×60%=1000×80%
∴x = 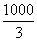 >300 ∴该同学加水未过量。
>300 ∴该同学加水未过量。
⑵设应加入浓度为20%的酒精y克,此时总溶液为(1000+300+y)克,浓度为60%,溶质(纯酒精)为(1000+300+y)×60%;原两种溶液的浓度分别为1000×80%、20%y,由混合前后溶质量不变,有(1000+300+y)×60%=1000×80%+20% ∴ y=50
5.数字问题
数字问题是常见的数学问题。一元一次方程应用题中的数字问题多是整数,要注意数位、数位上的数字、数值三者间的关系:任何数=∑(数位上的数字×位权),如两位数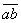 =10a+b;三位数
=10a+b;三位数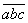 =100a+10b+c。在求解数字问题时要注意整体设元思想的运用。
=100a+10b+c。在求解数字问题时要注意整体设元思想的运用。
例12. 一个三位数,三个数位上的和是17,百位上的数比十位上的数大7,个位上的数是十位上的数的3倍。求这个数。
讲评:设这个数十位上的数字为x,则个位上的数字为3x,百位上的数字为(x+7),这个三位数则为100(x+7)+10x+3x。依题意有(x+7)+x+3x=17 ∴x=2
∴100(x+7)+10x+3x=900+20+6=926
例13. 一个六位数的最高位上的数字是1,如果把这个数字移到个位数的右边,那么所得的数等于原数的3倍,求原数。
讲评:这个六位数最高位上的数移到个位后,后五位数则相应整体前移1位,即每个数位上的数字被扩大10倍,可将后五位数看成一个整体设未知数。设除去最高位上数字1后的5位数为x,则原数为10
∴x = 42857 则原数为142857
6.调配(分配)与比例问题
调配与比例问题在日常生活中十分常见,比如合理安排工人生产,按比例选取工程材料,调剂人数或货物等。调配问题中关键是要认识清楚部分量、总量以及两者之间的关系。在调配问题中主要考虑“总量不变”;而在比例问题中则主要考虑总量与部分量之间的关系,或是量与量之间的比例关系。
例14.甲、乙两书架各有若干本书,如果从乙架拿100本放到甲架上,那么甲架上的书比乙架上所剩的书多5倍,如果从甲架上拿100本书放到乙架上,两架所有书相等。问原来每架上各有多少书?
讲评:本题难点是正确设未知数,并用含未知数的代数式将另一书架上书的本数表示出来。在调配问题中,调配后数量相等,即将原来多的一方多出的数量进行平分。由题设中“从甲书架拿100本书到乙书架,两架书相等”,可知甲书架原有的书比乙书架上原有的书多200本。故设乙架原有x本书,则甲架原有(x+200)本书。从乙架拿100本放到甲架上,乙架剩下的书为(x-100)本,甲架书变为(x+200)+100本。又甲架的书比乙架多5倍,即是乙架的六倍,有 (x+200)+100=6(x-100) ∴x=180 x+200=380
例15.教室内共有灯管和吊扇总数为13个。已知每条拉线管3个灯管或2个吊扇,共有这样的拉线5条,求室内灯管有多少个?
讲评:这是一道对开关拉线的分配问题。设灯管有x支,则吊扇有(13-x)个,灯管拉线为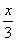 条,吊扇拉线为
条,吊扇拉线为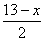 条,依题意“共有5条拉线”,有
条,依题意“共有5条拉线”,有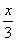 +
+
例16.某车间22名工人参加生产一种螺母和螺丝。每人每天平均生产螺丝120个或螺母200个,一个螺丝要配两个螺母,应分配多少名工人生产螺丝,多少名工人生产螺母,才能使每天生产的产品刚好配套?
讲评:产品配套(工人调配)问题,要根据产品的配套关系(比例关系)正确地找到它们间得数量关系,并依此作相等关系列出方程。本题中,设有x名工人生产螺母,生产螺母的个数为200x个,则有(22-x)人生产螺丝,生产螺丝的个数为120(22-x)个。由“一个螺丝要配两个螺母”即“螺母的个数是螺丝个数的2倍”,有 200x=2×120(22-x)
∴x=12 22-x=10
例17. 地板砖厂的坯料由白土、沙土、石膏、水按25∶2∶1∶6的比例配制搅拌而成。现已将前三种料称好,公5600千克,应加多少千克的水搅拌?前三种料各称了多少千克?
讲评:解决比例问题的一般方法是:按比例设未知数,并根据题设中的相等关系列出方程进行求解。本题中,由四种坯料比例25∶2∶1∶6,设四种坯料分别为25x、2x、x、6x千克,由前三种坯料共5600千克,有 25x+2x+x=5600
∴ x=200 25x=5000 2x=400 x=200 6x=1200
例18. 苹果若干个分给小朋友,每人m个余14个,每人9个,则最后一人得6个。问小朋友有几人?
讲评:这是一个分配问题。设小朋友x人,每人分m个苹果余14个,苹果总数为mx+14,每人9个苹果最后一人6个,则苹果总数为9(x-1)+6。苹果总数不变,有
mx+14=9(x-1)+6 ∴x= ∵x、m均为整数 ∴9-m=1 x=17
∵x、m均为整数 ∴9-m=1 x=17
例19. 出口1吨猪肉可以换5吨钢材,7吨猪肉价格与4吨砂糖的价格相等,现有288吨砂糖,把这些砂糖出口,可换回多少吨钢材?
讲评:本题可转换成一个比例问题。由猪肉∶钢材=1∶5,猪肉∶砂糖=7∶4,得猪肉∶钢材∶砂糖=7∶35∶4,设可换回钢材x吨,则有 x∶288=35∶4 ∴x=2620
7.需设中间(间接)未知数求解的问题
一些应用题中,设直接未知数很难列出方程求解,而根据题中条件设间接未知数,却较容易列出方程,再通过中间未知数求出结果。
例
20.甲、乙、丙、丁四个数的和是43,甲数的2倍加8,乙数的3倍,丙数的4倍,丁数的5倍减去4,得到的4个数却相等。求甲、乙、丙、丁四个数。
讲评:本题中要求4个量,在后面可用方程组求解。若用一元一次方程求解,如果设某个数为未知数,其余的数用未知数表示很麻烦。这里由甲、乙、丙、丁变化后得到的数相等,故设这个相等的数为x,则甲数为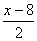 ,乙数为
,乙数为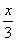 ,丙数为
,丙数为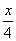 ,丁数为
,丁数为
∴ 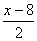 =14
=14
例21.某县中学生足球联赛共赛10轮(即每队均需比赛10场),其中胜1场得3分,平1场得1分,负1场得0分。向明中学足球队在这次联赛中所负场数比平场数少3场,结果公得19分。向明中学在这次联赛中胜了多少场?
讲评:本题中若直接将胜的场次设为未知数,无法用未知数的式子表示出负的场数和平的场数,但设平或负的场数,则可表示出胜的场数。故设平
x场,则负x-3场,胜10-(x+x-3)场,依题意有 3[10-(x+x-3)]+x=19 ∴x=4 ∴ 10-(x+x-3)=5
8.设而不求(设中间参数)的问题
一些应用题中,所给出的已知条件不够满足基本量关系式的需要,而且其中某些量不需要求解。这时,我们可以通过设出这个量,并将其看成已知条件,然后在计算中消去。这将有利于我们对问题本质的理解。
例22.一艘轮船从重庆到上海要5昼夜,从上海驶向重庆要7昼夜,问从重庆放竹牌到上海要几昼夜?(竹排的速度为水的流速)
分析:航行问题要抓住路程、速度、时间三个基本量,一般有两种已知量才能求出第三种未知量。本题中已知时间量,所求也是时间量,故需在路程和速度两个量中设一个中间参数才能列出方程。本题中考虑到路程量不变,故设两地路程为a公里,则顺水速度为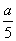 ,逆水速度为
,逆水速度为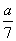 ,设水流速度为x,有
,设水流速度为x,有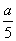 -x=
-x=
例23. 某校两名教师带若干名学生去旅游,联系两家标价相同的旅行社,经洽谈后,甲旅行社的优惠条件是:1名教师全部收费,其余7.5折收费;乙旅行社的优惠条件是:全部师生8折优惠。
⑴当学生人数等于多少人时,甲旅行社与乙旅行社收费价格一样?
⑵若核算结果,甲旅行社的优惠价相对乙旅行社的优惠价要便宜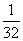 ,问学生人数是多少?
,问学生人数是多少?
讲评:在本题中两家旅行社的标价和学生人数都是未知量,又都是列方程时不可少的基本量,但标价不需求解。⑴中设标价为a元,学生人数x人,甲旅行社的收费为a+0.75a(x+1)元,乙旅行社收费为0.8a(x+2)元,有 a+0.75a(x+1)=0.8a(x+2) ∴ x=3
⑵中设学生人数为y人,甲旅行社收费为a+0.75a(x+1)元,乙旅行社收费为0.8a(x+2)元,有 0.8a(x+2)-[a+0.75a(x+1)]=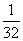 ×0.8a(x+2) ∴x=8。
×0.8a(x+2) ∴x=8。
| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |

