选用方程法设置未知数时应该注意的两个问题是:(1)以便于理解为准,设出来的未知数要便于列方程;(2)设题目所求的量为未知量。未知数设好后,在消除未知数时应该注意保留题目所求未知量,消去其它未知量,并且消未知数时注重整体代换。下面我们来看一些历年的真题:
【例题】
[例1]某公司,甲、乙两个营业部共有50人,其总,32人为男性,甲营业部男女比例为5:3,乙为2:1,问甲营业部有多少名女职员?( )
A. 18 B. 16 C. 12 D. 9
[答案]C
[解析]假设甲营业部男、女职员分别为5x、3x人,乙营业部男、女职员分别2y、y人,则:

[例2]甲、乙、丙、丁四人,其中每三个人的岁数之和分别是55、58、62、65。这四个人中年龄最小的是( )
A.7岁 B.10岁 C.15岁 D.18岁
[答案]C
[解析]假设四人的年龄分别为x、y、z、w岁,那么:
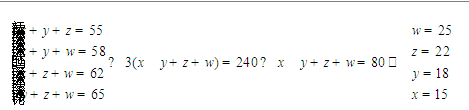
[注释]本题对称的给出了若干个方程,我们将所有方程直接相加,得到了所有未知数的总和,再用这个总和分别减去原有的四个方程,于是直接得到了四个未知数的解。这是一种典型的“整体法”解方程,我们在很多地方可以遇到这种情形,要求大家特别重视。
[例3]地上放着一个每一面上都有一个数的六面体箱子,对面两个数的和均为27,甲能看到顶面和两个侧面,这三个面上的数字之和是35;乙能看到顶面和另外两个侧面,且这三个面上的数字和为47。箱子贴地一面的数字是多少?
A.14 B.13 C.12 D.11
[答案]B
[解析]假设箱子的上、下、左、右、前、后面上的数字分别为x、27-x、y、27-y、z、27-z,甲看到的两个侧面如果是对着的两个侧面,那甲看到的三个面的数字之和应该等于乙看到的三个面的数字之和,与题意矛盾。于是,甲看到的两个侧面一定是相邻的两个侧面,我们不妨设甲看到的是上、左、前,乙看到的是上、右、后,那么:
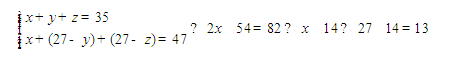
近年来,无论是国考还是省考,“牛吃草”问题出现频率较高,一般是采取“公式法”来进行解题,所谓“牛吃草”问题,就是当题目表述为某量以一定速度均匀增长,同时又以另一速度被均匀消耗,可以直接套用牛吃草问题公式:
原有草量=(牛数-单位时间长草量)×天数
下面我们来看一道该类问题:
[例4]有一块草地,每天草生长的速度相同。现在这片牧草可供16头牛吃20天,或者供80只羊吃12天。如果一头牛一天的吃草量相当于4只羊一天的吃草量,那么这片草地可供10头牛和60只羊一起吃多少天?
A.6天 B.8天 C.12天 D.15天
[答案]B
[解析]根据题设条件,我们将题目中的“羊”全部代换为“牛”。“80只羊吃12天”等价于“20头牛吃12天”;“10头牛和60只羊”等价于“25头牛”,可得:

在运用公式法直接套用公式进行解题时,难点在设置未知数和求解方程组,整体难度不高,但是在考试频率方面相对较高,需要考生在日后的学习中多加练习,提高解题速度。

