留学群专题频道数列求和公式推导栏目,提供与数列求和公式推导相关的所有资讯,希望我们所做的能让您感到满意!
等比数列是高中数学中一个十分重要的知识点,同时也是考试中一个常见的考点。下面是由留学群编辑为大家整理的“等比数列求和公式推导过程是什么”,仅供参考,欢迎大家阅读本文。
等比数列前n项和公式

公式中a1为数列首项,q为等比数列的公比,Sn为前n项和。
等比数列求和公式推导
方法1:
第一项:a1, 公比:q
a1=a1
a2=a1•q¬
a3=a1•q¬2
a4=a1•q¬3
an=a1•q¬n-1
an+1=a1•qn¬
Sn+1=a1+a1•q¬+a1•q¬2+a1•q¬3+…+a1•q¬n-1+ a1•qn¬
Sn+1=a1+q(a1•q¬+a1•q¬2+a1•q¬3+…+a1•q¬n-1)
Sn+ a1•qn =a1+q•Sn
Sn-q•Sn= a1-a1•qn
Sn= a1•(1- qn)/(1-q)
方法2:
(1)Sn=a1+a2+a3+...+an(公比为q)
(2)q*Sn=a1*q+a2*q+a3*q+...+an*q
=a2+a3+a4+...+a(n+1)
(3)Sn-q*Sn=a1-a(n+1)
(4)(1-q)Sn=a1-a1*q^n
(5)Sn=(a1-a1*q^n)/(1-q)
(6)Sn=(a1-an*q)/(1-q)
(7)Sn=a1(1-q^n)/(1-q)
(8)Sn=k*(1-q^n)~y=k*(1-a^x)
拓展阅读:等比数列求通项方法

等差数列是数学中一个很重要的知识点,也是一个十分常见的考点。下面是由留学群编辑为大家整理的“等差数列前n项和公式推导”,仅供参考,欢迎大家阅读本文。
等差数列求和公式


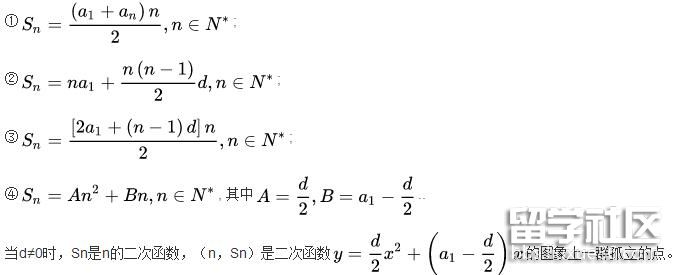
推导过程
(1)从通项公式可以看出,a(n)是n的一次函数(d≠0)或常数函数(d=0),(n,an)排在一条直线上,由前n项和公式知,S(n)是n的二次函数(d≠0)或一次函数(d=0,a1≠0),且常数项为0。
(2)从等差数列的定义、通项公式,前n项和公式还可推出:a(1)+a(n)=a(2)+a(n-1)=a(3)+a(n-2)=…=a(k)+a(n-k+1),(类似:p(1)+p(n)=p(2)+p(n-1)=p(3)+p(n-2)=。。。=p(k)+p(n-k+1)),k∈{1,2,…,n}。
(3)若m,n,p,q∈N*,且m+n=p+q,则有a(m)+a(n)=a(p)+a(q),S(2n-1)=(2n-1)*a(n),S(2n+1)=(2n+1)*a(n+1),S(k),S(2k)-S(k),S(3k)-S(2k),…,S(n)*k-S(n-1)*k…成等差数列,等等。若m+n=2p,则a(m)+a(n)=2*a(p)。
...数列求和公式推导推荐访问