留学群专题频道点到直线的距离公式栏目,提供与点到直线的距离公式相关的所有资讯,希望我们所做的能让您感到满意!
点到直线的公式:d=│(Axo+Byo+C)/√(A²+B²)│,那么这个公式的推导过程是怎样的呢?下面是由留学群编辑为大家整理的“点到直线的距离公式推导过程有哪些”,仅供参考,欢迎大家阅读本文。
点到直线的距离公式的七种推导方法







11-15
点到直线的距离公式是数学中一个重要的知识点,大家还记得是在什么时候学的吗?公式又是怎样的呢?下面是由留学群编辑为大家整理的“点到直线的距离公式是在初中学的吗”,仅供参考,欢迎大家阅读本文。
点到直线的距离公式是在初中学的吗
点到直线的距离公式是在人教版教材必修2中,一般是在高一学。
点到直线的距离公式点到直线的距离,即过这一点做目标直线的垂线,由这一点至垂足的距离。
设直线L的方程为Ax+By+C=0,点P的坐标为(x0,y0),则点P到直线L的距离为:
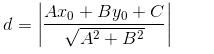
考虑点(x0,y0,z0)与空间直线x-x1/l=y-y1/m=z-z1/n,有s=|(x1-x0,y1-y0,z1-z0)×(l,m,n)|/√(l²+m²+n²)
d=√((x1-x0)²+(y1-y0)²+(z1-z0)²-s²)
点到直线的距离公式推导方法

11-05
点到直线的距离公式是同学们在做题时经常会用到的,那么点到直线的距离公式有哪些,又是怎样推导出来的呢?下面是由留学群编辑为大家整理的“点到直线的距离公式,点到直线的距离公式推导方法”,仅供参考,欢迎大家阅读本文。
点到直线的距离公式
距离公式:d=│(Axo+Byo+C)/√(A²+B²)│公式描述:公式中的直线方程为Ax+By+C=0,点P的坐标为(x0,y0)。点到直线的距离,即过这一点做目标直线的垂线,由这一点至垂足的距离。
过点做直线的垂线,所得的垂线段即点到直线的距离。
如若直线的方程为:ax+by+c=0,点坐标为:(x,y)
则有距离公式|ax+by+c|/√(a^2+b^2)
点到直线距离是指垂线段的长。求出过点M且与已知直线aX+bY+c=0(a、b均不为零)垂直的直线方程,而后联立方程组,求出垂足N点的坐标,然后利用两点间的距离公式求出点到直线的距离。
点到直线的距离公式推导方法

08-03
数学公式公式需要理解记忆,那么点到直线的距离公式是初中学的吗?下面是由留学群小编为大家整理的“点到直线的距离公式是初中学的吗”,仅供参考,欢迎大家阅读。
不是初中学的,是高中学的。点到直线的距离公式是d=|Ax0+By0+C|/√(A²+B²)。
直线是一个点在平面或空间沿着一定方向和其相反方向运动的轨迹;是一条不弯曲的线。直线是几何学的基本概念,在不同的几何学体系中有着不同的描述。直线在这里主要描述欧几里得空间中的直线。其他曲率非零状况下的直线,请参考非欧几里得几何。
点到直线的距离公式推导过程
定义法证:根据定义,点P(x₀,y₀)到直线l:Ax+By+C=0的距离是点P到直线l的垂线段的长,设点P到直线的垂线为l',垂足为Q,则l'的斜率为B/A则l'的解析式为y-y₀=(B/A)(x-x₀)把l和l'联立得l与l'的交点Q的坐标为((B^2x₀-ABy₀-AC)/(A^2+B^2), (A^2y₀-ABx₀-BC)/(A^2+B^2))由两点间距离公式得:
PQ^2=[(B^2x₀-ABy₀-AC)/(A^2+B^2)-x0]^2
+[(A^2y₀-ABx₀-BC)/(A^2+B^2)-y0]^2
=[(-A^2x₀-ABy₀-AC)/(A^2+B^2)]^2
+[(-ABx₀-B^2y₀-BC)/(A^2+B^2)]^2
=[A(-By₀-C-Ax₀)/(A^2+B^2)]^2
+[B(-Ax₀-C-By₀)/(A^2+B^2)]^2
=A^2(Ax₀+By₀+C)^2/(A^2+B^2)^2
+B^2(Ax₀+By₀+C)^2/(A^2+B^2)^2
=(A^2+B^2)(Ax₀+By₀+C)^2/(A^2+B^2)^2
=(Ax₀+By₀+C)^2/(A^2+B^2)
所以PQ=|Ax₀+By₀+C|/√(A^2+B^2),公式得证。
1.要有良好的数学学习方法和习惯
良好的数学学习习惯,会减轻数学学习的难度,要学会把课堂知识用自己特殊方法记忆下来,那就要做到认真预习、专心上课、及时复习、独立作业、系统小结。
2.掌握常用的数学思想和方法
做数学题时,也要注意解题思维策略问题,经常要思考:选择什么角度来进入,应遵循什么原则性的东西,是否可以运用哪些数学公式来做这些题。
3.慢慢养成“以我为主”的学习模式
学习数学就要积极主动地参与学习过程,养成实事求是的科学态度,独立思考、勇于探索的创新精神;对课本知识既要能钻进去,又要能跳出来,结合自身特点,寻找最佳学习方法。
4.针对自己的学习情况,采取一些具体的措施
(1)记数学笔记,特别是对概念理解的不同侧面和数学规律,教师在课堂中拓展的课外知识。
(2)建立数学纠错本。把平时容易出现错误的知识...
数学公式公式需要理解记忆,那么点到直线的距离公式推导过程是什么呢?下面是由留学群小编为大家整理的“点到直线的距离公式推导过程”,仅供参考,欢迎大家阅读。
点到直线的距离公式推导过程
定义法证:根据定义,点P(x₀,y₀)到直线l:Ax+By+C=0的距离是点P到直线l的垂线段的长,设点P到直线的垂线为l',垂足为Q,则l'的斜率为B/A则l'的解析式为y-y₀=(B/A)(x-x₀)把l和l'联立得l与l'的交点Q的坐标为((B^2x₀-ABy₀-AC)/(A^2+B^2), (A^2y₀-ABx₀-BC)/(A^2+B^2))由两点间距离公式得:
PQ^2=[(B^2x₀-ABy₀-AC)/(A^2+B^2)-x0]^2
+[(A^2y₀-ABx₀-BC)/(A^2+B^2)-y0]^2
=[(-A^2x₀-ABy₀-AC)/(A^2+B^2)]^2
+[(-ABx₀-B^2y₀-BC)/(A^2+B^2)]^2
=[A(-By₀-C-Ax₀)/(A^2+B^2)]^2
+[B(-Ax₀-C-By₀)/(A^2+B^2)]^2
=A^2(Ax₀+By₀+C)^2/(A^2+B^2)^2
+B^2(Ax₀+By₀+C)^2/(A^2+B^2)^2
=(A^2+B^2)(Ax₀+By₀+C)^2/(A^2+B^2)^2
=(Ax₀+By₀+C)^2/(A^2+B^2)
所以PQ=|Ax₀+By₀+C|/√(A^2+B^2),公式得证。
拓展阅读:数学公式如何记忆
1、连锁记忆法
就是对将要进行记忆的词语,进行一一串接,由一个词语想到另一个词语,这种记忆的关键在于串接的链条的结实程度,例如,我们来记忆书桌,篮球,高楼三组词语,首先,书桌和篮球链接,书桌下的篮球慢慢变大,把书桌顶到房顶,然后篮球和高楼,大大的篮球样的球从高空落下,把高楼砸的粉碎。
2、编故事记忆法
首先对需记忆内容进行提取关键词,然后通过形象,生动的故事把关键词串接起来,帮助记忆。
3、定桩法
首先用定桩,有身体桩、数字桩、罗马房间等,然后需记忆内容与桩子挂钩,达到记忆的目的
4、口诀记忆法
利用口诀,顺口溜记忆,如,1851年,秀全起义在金田,1839.6月3,林则徐硝烟虎门滩等。
5、首字母记忆法,提取首字母减少记忆负担。
6、归纳记忆法,把同类内容记忆,按照大脑存储原理。
7、图表记忆法,把所需要记忆内容用形象表现出来,利用右脑帮助记忆。
8、音乐记忆法,利用a波段音乐,调动潜意识帮助记忆。
9、复述记忆法,用尝试回忆的方法来帮助记忆。
10、联想记忆法,利用谐音等手段,辅助记忆。
...02-01
想要了解点到直线的距离公式的小伙伴,赶紧来瞧瞧吧!下面由留学群小编为你精心准备了“点到直线的距离公式是什么”,本文仅供参考,持续关注本站将可以持续获取更多的资讯!
点到直线的距离公式
点到直线的距离,即过这一点做目标直线的垂线,由这一点至垂足的距离。
设直线L的方程为Ax+By+C=0,点P的坐标为(x0,y0),则点P到直线L的距离为:

考虑点(x0,y0,z0)与空间直线x-x1/l=y-y1/m=z-z1/n,有s=|(x1-x0,y1-y0,z1-z0)×(l,m,n)|/√(l²+m²+n²)。
d=√((x1-x0)²+(y1-y0)²+(z1-z0)²-s²)。
拓展阅读:点到直线的距离定义
从直线外一点到这条直线的垂线段长度,叫点到直线的距离。
点和直线的位置关系
点与直线只有两种位置关系:一种是点在直线上,一种是点在直线外。点是最简单的形,是几何图形最基本的组成部分。在空间中作为1个零维的对象。在其它领域中,点也作为讨论的对象。直线由无数个点构成。直线是面的组成成分,并继而组成体。没有端点,向两端无限延长,长度无法度量。
过一点可以画几条直线
直线由无数个点构成。直线是面的组成成分,并继而组成体。没有端点,向两端无限延长,长度无法度量。经过一个点可以画无数条直线。经过两个点可以画一条直线。
直线与线段和射线的区别
1、直线无端点,长度无限,向两方无限延伸。
2、射线只有一个端点,长度无限,向一方无限延伸。
3、线段有两个端点,长度有限。
...点到直线的距离公式推荐访问