留学群专题频道等差数列前n项和公式栏目,提供与等差数列前n项和公式相关的所有资讯,希望我们所做的能让您感到满意!
04-21
有的数学公式算法还是比较复杂的,很多公式求和之类的,也不是一步两步就可以算出结果的哦,留学群的小编今天就带你们去了解一下这个等差数列前n项和公式方法有哪些。
1、用倒序相加法求数列的前n项和。
如果一个数列{an},与首末项等距的两项之和等于首末两项之和,可采用把正着写与倒着写的两个和式相加,就得到一个常数列的和,这一求和方法称为倒序相加法。
2、用公式法求数列的前n项和(等差数列公式求和公式:Sn=n(a1+an)/2或Sn=na1+n(n-1)d/2)。
对等差数列,求前n项和Sn可直接用等差数列的前n项和公式进行求解。运用公式求解的注意事项:首先要注意公式的应用范围,确定公式适用于这个数列之后,再计算。
3、用裂项相消法求数列的前n项和。
裂项相消法是将数列的一项拆成两项或多项,使得前后项相抵消,留下有限项,从而求出数列的前n项和。
4、用构造法求数列的前n项和。
所谓构造法就是先根据数列的结构及特征进行分析,找出数列的通项的特征,构造出我们熟知的基本数列的通项的特征形式,从而求出数列的前n项和。
等差数列是指从第二项起,每一项与它的前一项的差等于同一个常数的一种数列,常用A、P表示。这个常数叫做等差数列的公差,公差常用字母d表示。
例如:1,3,5,7,9……2n-1。通项公式为:an=a1+(n-1)*d。首项a1=1,公差d=2。前n项和公式为:Sn=a1*n+[n*(n-1)*d]/2或Sn=[n*(a1+an)]/2。注意:以上n均属于正整数。
等差数列前n项和公式方法有哪些?什么是等差数列?留学群的小编今天就先和你们普及到这里了哦,更多相关的数学公式我们下期再分享。
推荐阅读:
...
等差数列是数学中一个很重要的知识点,也是一个十分常见的考点。下面是由留学群编辑为大家整理的“等差数列前n项和公式推导”,仅供参考,欢迎大家阅读本文。
等差数列求和公式


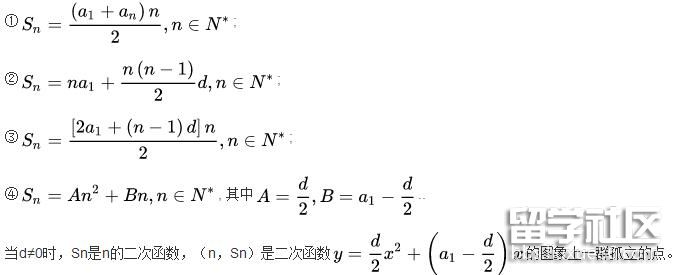
推导过程
(1)从通项公式可以看出,a(n)是n的一次函数(d≠0)或常数函数(d=0),(n,an)排在一条直线上,由前n项和公式知,S(n)是n的二次函数(d≠0)或一次函数(d=0,a1≠0),且常数项为0。
(2)从等差数列的定义、通项公式,前n项和公式还可推出:a(1)+a(n)=a(2)+a(n-1)=a(3)+a(n-2)=…=a(k)+a(n-k+1),(类似:p(1)+p(n)=p(2)+p(n-1)=p(3)+p(n-2)=。。。=p(k)+p(n-k+1)),k∈{1,2,…,n}。
(3)若m,n,p,q∈N*,且m+n=p+q,则有a(m)+a(n)=a(p)+a(q),S(2n-1)=(2n-1)*a(n),S(2n+1)=(2n+1)*a(n+1),S(k),S(2k)-S(k),S(3k)-S(2k),…,S(n)*k-S(n-1)*k…成等差数列,等等。若m+n=2p,则a(m)+a(n)=2*a(p)。
...08-04
等差数列前n项和公式推导是怎样的呢?感兴趣的小伙伴快来和小编一起看看吧。下面是由留学群小编为大家整理的“等差数列前n项和公式推导”,仅供参考,欢迎大家阅读。
等差数列前n项和公式推导
1.Sn=a1+a2+......an-1+an也可写成
Sn=an+an-1+......a2+a1
两式相加得:
2Sn=(a1+an)+(a2+an-1)+......(an+a1)
=n(a1+an)
所以Sn=[n(a1+an)]/2。
2.如果已知等差数列的首项为a1,公差为d,项数为n,
则 an=a1+(n-1)d代入公式公式一得,
Sn=na1+ [n(n+1)d]/2。
拓展阅读:等差数列性质
1.数列为等差数列的重要条件是:数列的前n项和S可以写成S=an^2+bn的形式(其中a、b为常数)。
2.在等差数列中,当项数为2n(n∈N+)时,S偶-S奇=nd,S奇÷S偶=an÷a(n+1);当项数为(2n-1)(n∈N+)时,S奇—S偶=a(中),S奇-S偶=项数*a(中),S奇÷S偶=n÷(n-1)。
3.若数列为等差数列,则Sn,S2n-Sn,S3n-S2n,…仍然成等差数列,公差为k^2d。
4.若数列{an}与{bn}均为等差数列,且前n项和分别是Sn和Tn,则am/bm=S2m-1/T2m-1。
5.在等差数列中,S=a,S=b(n>m),则S=(a-b)。
6.等差数列中,是n的一次函数,且点(n,)均在直线y=x+(a-)上。
7.记等差数列的前n项和为S.①若a>0,公差d<0,则当a≥0且an+1≤0时,S最大;②若a<0,公差d>0,则当a≤0且an+1≥0时,S最小。
8.若等差数列S(p)=q,S(q)=p,则S(p+q)=-(p+q)。
...等差数列前n项和公式推荐访问