留学群专题频道距离公式栏目,提供与距离公式相关的所有资讯,希望我们所做的能让您感到满意!
04-21
两点间距离公式是什么?对于数学知识有些朋友也是觉得很头疼,今天留学群给大家分享一下关于两点间距离公式的相关知识点,感兴趣的朋友们进来文章了解一下吧。
两点间距离公式常用于函数图形内求两点之间距离、求点的坐标的基本公式,是距离公式之一。两点间距离公式叙述了点和点之间距离的关系。
两点间距离公式是∣AB∣=√[(x1-x2)²+(y1-y2)²]。
两点间距离公式叙述了点和点之间距离的关系。
设两个点A、B以及坐标分别为:A(X1,Y1)、B(X2,Y2)则A和B两点之间的距离为:∣AB∣=√[(x1-x2)²+(y1-y2)²]。两点距离公式是常用于函数图形内求两点之间距离、求点的坐标的基本公式,是距离公式之一。
两点间距离公式推论:
已知AB两点坐标为A(x1,y1),B(x2,y2)。过A做一直线与X轴平行,过B做一直线与Y轴平行,两直线交点为C。则AC垂直于BC(因为X轴垂直于Y轴);则三角形ACB为直角三角形,
由勾股定理得:AB^2=AC^2+BC^2;故AB=根号下AC^2+BC^2,即两点间距离公式。
点到直线的距离:
直线Ax+By+C=0 坐标(x0,y0)那么这点到这直线的距离就为:d=│Ax0+By0+C│/根号(A^2+B^2)。
公式描述:
公式中的直线方程为Ax+By+C=0,点P的坐标为(x0,y0)。连接直线外一点与直线上各点的所有线段中,垂线段最短,这条垂线段的长度,叫做点到直线的距离。
勾股定理,是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理,也有人称商高定理。
勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一。勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
在中国,周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例。在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他们用演绎法证明了直角三角形斜边平方等于两直角边平方之和。
看完上文所分享的两点间距离公式知识之后,大家对于两点间距离公式知识也是有了更深的认识和了解,希望这些内容可以给你们带来启发。
推荐阅读:
...
点到直线的公式:d=│(Axo+Byo+C)/√(A²+B²)│,那么这个公式的推导过程是怎样的呢?下面是由留学群编辑为大家整理的“点到直线的距离公式推导过程有哪些”,仅供参考,欢迎大家阅读本文。
点到直线的距离公式的七种推导方法







11-15
点到直线的距离公式是数学中一个重要的知识点,大家还记得是在什么时候学的吗?公式又是怎样的呢?下面是由留学群编辑为大家整理的“点到直线的距离公式是在初中学的吗”,仅供参考,欢迎大家阅读本文。
点到直线的距离公式是在初中学的吗
点到直线的距离公式是在人教版教材必修2中,一般是在高一学。
点到直线的距离公式点到直线的距离,即过这一点做目标直线的垂线,由这一点至垂足的距离。
设直线L的方程为Ax+By+C=0,点P的坐标为(x0,y0),则点P到直线L的距离为:
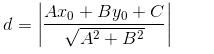
考虑点(x0,y0,z0)与空间直线x-x1/l=y-y1/m=z-z1/n,有s=|(x1-x0,y1-y0,z1-z0)×(l,m,n)|/√(l²+m²+n²)
d=√((x1-x0)²+(y1-y0)²+(z1-z0)²-s²)
点到直线的距离公式推导方法

11-05
点到直线的距离公式是同学们在做题时经常会用到的,那么点到直线的距离公式有哪些,又是怎样推导出来的呢?下面是由留学群编辑为大家整理的“点到直线的距离公式,点到直线的距离公式推导方法”,仅供参考,欢迎大家阅读本文。
点到直线的距离公式
距离公式:d=│(Axo+Byo+C)/√(A²+B²)│公式描述:公式中的直线方程为Ax+By+C=0,点P的坐标为(x0,y0)。点到直线的距离,即过这一点做目标直线的垂线,由这一点至垂足的距离。
过点做直线的垂线,所得的垂线段即点到直线的距离。
如若直线的方程为:ax+by+c=0,点坐标为:(x,y)
则有距离公式|ax+by+c|/√(a^2+b^2)
点到直线距离是指垂线段的长。求出过点M且与已知直线aX+bY+c=0(a、b均不为零)垂直的直线方程,而后联立方程组,求出垂足N点的坐标,然后利用两点间的距离公式求出点到直线的距离。
点到直线的距离公式推导方法

两点间距离公式是什么呢?感兴趣的小伙伴快来和小编一起看看吧。下面是由留学群小编为大家整理的“两点间距离公式是什么”,仅供参考,欢迎大家阅读。
两点间距离公式是什么
两点间距离公式常用于函数图形内求两点之间距离、求点的坐标的基本公式,是距离公式之一。两点间距离公式叙述了点和点之间距离的关系。
两点的坐标是(x1,y1)和(x2,y2),则两点之间的距离公式为 d=√[(x1-x2)2+(y1-y2)2]
注意特例:
当x1=x2时,两点间距离为|y1-y2|;当y1=y2时,两点间距离为|x1-x2|。
当然,不管特例,全部照代公式,结果都是对的,但没有必要时,不要增加自己的运算量。
空间中两点间的距离公式
在空间直角坐标系统中,点P(x1,y1,z1)和点Q(x2,y2,z2)的距离公式:
d=√(x2-x1)2+(y2-y1)2+(z2-z1)2;
推导过程:
空间任意两点A(x1,y1,z1),P(x2,y2,z2)作长方体使A,P为其对角线的顶点。
由已知得:
C(x2,y1,z1),B(x2,y2,z1)
|AP|2=|AC|2+|CB|2+|BP|2
|AP|=√(x2-x1)2+(y2-y1)2+(z2-z1)2
即是:空间两点间的距离公式
拓展阅读:点到直线的距离公式
设直线L的方程为Ax+By+C=0,点P的坐标为(x0,y0),则点P到直线L的距离为:|AX0+BY0+C|/√A2+B2。点向式:知道直线上一点(x0,y0)和方向向量(u,v)即可使用,(x-x0)/u=(y-y0)/v(u≠0,v≠0)。
点到直线的距离,即过这一点做目标直线的垂线,由这一点至垂足的距离。总公式为:设直线L的方程为Ax+By+C=0,点P的坐标为(x0,y0),则点P到直线L的距离为:|AX0+BY0+C|/√A2+B2。考虑点(x0,y0,z0)与空间直线x-x1/l=y-y1/m=z-z1/n,有d=|(x1-x0,y1-y0,z1-z0)×(l,m,n)|/√(l²+m²+n²)。
点向式:知道直线上一点(x0,y0)和方向向量(u,v)即可使用,(x-x0)/u=(y-y0)/v(u≠0,v≠0)。例题:2x-3y+4=0,2(x+2)=3y,∴(x+2)/3=y/2,为所求。
...08-03
数学公式公式需要理解记忆,那么点到直线的距离公式是初中学的吗?下面是由留学群小编为大家整理的“点到直线的距离公式是初中学的吗”,仅供参考,欢迎大家阅读。
不是初中学的,是高中学的。点到直线的距离公式是d=|Ax0+By0+C|/√(A²+B²)。
直线是一个点在平面或空间沿着一定方向和其相反方向运动的轨迹;是一条不弯曲的线。直线是几何学的基本概念,在不同的几何学体系中有着不同的描述。直线在这里主要描述欧几里得空间中的直线。其他曲率非零状况下的直线,请参考非欧几里得几何。
点到直线的距离公式推导过程
定义法证:根据定义,点P(x₀,y₀)到直线l:Ax+By+C=0的距离是点P到直线l的垂线段的长,设点P到直线的垂线为l',垂足为Q,则l'的斜率为B/A则l'的解析式为y-y₀=(B/A)(x-x₀)把l和l'联立得l与l'的交点Q的坐标为((B^2x₀-ABy₀-AC)/(A^2+B^2), (A^2y₀-ABx₀-BC)/(A^2+B^2))由两点间距离公式得:
PQ^2=[(B^2x₀-ABy₀-AC)/(A^2+B^2)-x0]^2
+[(A^2y₀-ABx₀-BC)/(A^2+B^2)-y0]^2
=[(-A^2x₀-ABy₀-AC)/(A^2+B^2)]^2
+[(-ABx₀-B^2y₀-BC)/(A^2+B^2)]^2
=[A(-By₀-C-Ax₀)/(A^2+B^2)]^2
+[B(-Ax₀-C-By₀)/(A^2+B^2)]^2
=A^2(Ax₀+By₀+C)^2/(A^2+B^2)^2
+B^2(Ax₀+By₀+C)^2/(A^2+B^2)^2
=(A^2+B^2)(Ax₀+By₀+C)^2/(A^2+B^2)^2
=(Ax₀+By₀+C)^2/(A^2+B^2)
所以PQ=|Ax₀+By₀+C|/√(A^2+B^2),公式得证。
1.要有良好的数学学习方法和习惯
良好的数学学习习惯,会减轻数学学习的难度,要学会把课堂知识用自己特殊方法记忆下来,那就要做到认真预习、专心上课、及时复习、独立作业、系统小结。
2.掌握常用的数学思想和方法
做数学题时,也要注意解题思维策略问题,经常要思考:选择什么角度来进入,应遵循什么原则性的东西,是否可以运用哪些数学公式来做这些题。
3.慢慢养成“以我为主”的学习模式
学习数学就要积极主动地参与学习过程,养成实事求是的科学态度,独立思考、勇于探索的创新精神;对课本知识既要能钻进去,又要能跳出来,结合自身特点,寻找最佳学习方法。
4.针对自己的学习情况,采取一些具体的措施
(1)记数学笔记,特别是对概念理解的不同侧面和数学规律,教师在课堂中拓展的课外知识。
(2)建立数学纠错本。把平时容易出现错误的知识...
数学公式公式需要理解记忆,那么点到直线的距离公式推导过程是什么呢?下面是由留学群小编为大家整理的“点到直线的距离公式推导过程”,仅供参考,欢迎大家阅读。
点到直线的距离公式推导过程
定义法证:根据定义,点P(x₀,y₀)到直线l:Ax+By+C=0的距离是点P到直线l的垂线段的长,设点P到直线的垂线为l',垂足为Q,则l'的斜率为B/A则l'的解析式为y-y₀=(B/A)(x-x₀)把l和l'联立得l与l'的交点Q的坐标为((B^2x₀-ABy₀-AC)/(A^2+B^2), (A^2y₀-ABx₀-BC)/(A^2+B^2))由两点间距离公式得:
PQ^2=[(B^2x₀-ABy₀-AC)/(A^2+B^2)-x0]^2
+[(A^2y₀-ABx₀-BC)/(A^2+B^2)-y0]^2
=[(-A^2x₀-ABy₀-AC)/(A^2+B^2)]^2
+[(-ABx₀-B^2y₀-BC)/(A^2+B^2)]^2
=[A(-By₀-C-Ax₀)/(A^2+B^2)]^2
+[B(-Ax₀-C-By₀)/(A^2+B^2)]^2
=A^2(Ax₀+By₀+C)^2/(A^2+B^2)^2
+B^2(Ax₀+By₀+C)^2/(A^2+B^2)^2
=(A^2+B^2)(Ax₀+By₀+C)^2/(A^2+B^2)^2
=(Ax₀+By₀+C)^2/(A^2+B^2)
所以PQ=|Ax₀+By₀+C|/√(A^2+B^2),公式得证。
拓展阅读:数学公式如何记忆
1、连锁记忆法
就是对将要进行记忆的词语,进行一一串接,由一个词语想到另一个词语,这种记忆的关键在于串接的链条的结实程度,例如,我们来记忆书桌,篮球,高楼三组词语,首先,书桌和篮球链接,书桌下的篮球慢慢变大,把书桌顶到房顶,然后篮球和高楼,大大的篮球样的球从高空落下,把高楼砸的粉碎。
2、编故事记忆法
首先对需记忆内容进行提取关键词,然后通过形象,生动的故事把关键词串接起来,帮助记忆。
3、定桩法
首先用定桩,有身体桩、数字桩、罗马房间等,然后需记忆内容与桩子挂钩,达到记忆的目的
4、口诀记忆法
利用口诀,顺口溜记忆,如,1851年,秀全起义在金田,1839.6月3,林则徐硝烟虎门滩等。
5、首字母记忆法,提取首字母减少记忆负担。
6、归纳记忆法,把同类内容记忆,按照大脑存储原理。
7、图表记忆法,把所需要记忆内容用形象表现出来,利用右脑帮助记忆。
8、音乐记忆法,利用a波段音乐,调动潜意识帮助记忆。
9、复述记忆法,用尝试回忆的方法来帮助记忆。
10、联想记忆法,利用谐音等手段,辅助记忆。
...05-07
在数学课堂学习中,我们会学到两直线间的距离公式,那么两直线间的距离公式是什么呢。以下是由留学群编辑为大家整理的“两直线间的距离公式是什么”,仅供参考,欢迎大家阅读。
两平行线之间的距离公式:d=|C1-C2|/√(A²+B²)。两平行线方程分别是:Ax+By+C1=0和Ax+By+C2=0。
两平行线之间的距离公式
设两条直线方程为
Ax+By+C1=0
Ax+By+C2=0
则其距离公式为|C1-C2|/√(A²+B²)
推导:两平行直线间的距离就是从一条直线上任一点到另一条直线的距离,设点P(a,b)在直线Ax+By+C1=0上,则满足Aa+Bb+C1=0,即Aa+Bb=-C1,由点到直线距离公式,P到直线Ax+By+C2=0距离为
d=|Aa+Bb+C2|/√(A²+B²)
=|-C1+C2|/√(A²+B²)
=|C1-C2|/√(A²+B²)
学习数学的方法
一)、课内重视听讲,课后及时复习。
新知识的接受,数学能力的培养主要在课堂上进行,所以要特点重视课内的学习效率,寻求正确的学习方法。上课时要紧跟老师的思路,积极展开思维预测下面的步骤,比较自己的解题思路与教师所讲有哪些不同。特别要抓住基础知识和基本技能的学习,课后要及时复习不留疑点。首先要在做各种习题之前将老师所讲的知识点回忆一遍,正确掌握各类公式的推理过程,应尽量回忆而不采用不清楚立即翻书之举。认真独立完成作业,勤于思考,从某种意义上讲,应不造成不懂即问的学习作风,对于有些题目由于自己的思路不清,一时难以解出,应让自己冷静下来认真分析题目,尽量自己解决。在每个阶段的学习中要进行整理和归纳总结,把知识的点、线、面结合起来交织成知识网络,纳入自己的知识体系。
二)、适当多做题,养成良好的解题习惯。
要想学好数学,多做题是难免的,熟悉掌握各种题型的解题思路。刚开始要从基础题入手,以课本上的习题为准,反复练习打好基础,再找一些课外的习题,以帮助开拓思路,提高自己的分析、解决能力,掌握一般的解题规律。对于一些易错题,可备有错题集,写出自己的解题思路和正确的解题过程两者一起比较找出自己的错误所在,以便及时更正。在平时要养成良好的解题习惯。让自己的精力高度集中,使大脑兴奋,思维敏捷,能够进入最佳状态,在考试中能运用自如。实践证明:越到关键时候,你所表现的解题习惯与平时练习无异。如果平时解题时随便、粗心、大意等,往往在大考中充分暴露,故在平时养成良好的解题习惯是非常重要的。
三)、调整心态,正确对待考试。
首先,应把主要精力放在基础知识、基本技能、基本方法这三个方面上,因为每次考试占绝大部分的也是基础性的题目,而对于那些难题及综合性较强的题目作为调剂,认真思考,尽量让自己理出头绪,做完题后要总结归纳。调整好自己的心态,使自己在任何时候镇静,思路有条不紊,克服浮躁的情绪。特别是对自己要有信心,永远鼓励自己,除了自己,谁也不能把我打倒,要有自己不垮,谁也不能打垮我的自豪感。
02-01
想要了解点到直线的距离公式的小伙伴,赶紧来瞧瞧吧!下面由留学群小编为你精心准备了“点到直线的距离公式是什么”,本文仅供参考,持续关注本站将可以持续获取更多的资讯!
点到直线的距离公式
点到直线的距离,即过这一点做目标直线的垂线,由这一点至垂足的距离。
设直线L的方程为Ax+By+C=0,点P的坐标为(x0,y0),则点P到直线L的距离为:

考虑点(x0,y0,z0)与空间直线x-x1/l=y-y1/m=z-z1/n,有s=|(x1-x0,y1-y0,z1-z0)×(l,m,n)|/√(l²+m²+n²)。
d=√((x1-x0)²+(y1-y0)²+(z1-z0)²-s²)。
拓展阅读:点到直线的距离定义
从直线外一点到这条直线的垂线段长度,叫点到直线的距离。
点和直线的位置关系
点与直线只有两种位置关系:一种是点在直线上,一种是点在直线外。点是最简单的形,是几何图形最基本的组成部分。在空间中作为1个零维的对象。在其它领域中,点也作为讨论的对象。直线由无数个点构成。直线是面的组成成分,并继而组成体。没有端点,向两端无限延长,长度无法度量。
过一点可以画几条直线
直线由无数个点构成。直线是面的组成成分,并继而组成体。没有端点,向两端无限延长,长度无法度量。经过一个点可以画无数条直线。经过两个点可以画一条直线。
直线与线段和射线的区别
1、直线无端点,长度无限,向两方无限延伸。
2、射线只有一个端点,长度无限,向一方无限延伸。
3、线段有两个端点,长度有限。
...
还不清楚两点间的距离公式的小伙伴,赶紧来瞧瞧吧!下面由留学群小编为你精心准备了“两点之间的距离公式 点的定义”,本文仅供参考,持续关注本站将可以持续获取更多的资讯!
两点之间的距离公式
两点间距离公式常用于函数图形内求两点之间距离、求点的坐标的基本公式,是距离公式之一。两点间距离公式叙述了点和点之间距离的关系。两点的坐标是(x1,y1)和(x2,y2),则两点之间的距离公式为d=根号[(x1-x2)^2+(y1-y2)^2]。
点的定义
点是最简单的形,是几何图形最基本的组成部分。在空间中作为1个零维的对象。在其他领域中,点也作为讨论的对象。在欧氏几何中,点是空间中只有位置,没有大小的图形。点是整个欧氏几何的基础。
拓展阅读:点和直线的位置关系
点与直线只有两种位置关系:一种是点在直线上,一种是点在直线外。点是最简单的形,是几何图形最基本的组成部分。在空间中作为1个零维的对象。在其它领域中,点也作为讨论的对象。直线由无数个点构成。直线是面的组成成分,并继而组成体。没有端点,向两端无限延长,长度无法度量。
点到面的距离公式是什么
距离=|Ax0+By0+Cz0+D|/√(A²+B²+C²)。点在几何学上指没有长、宽、厚而只有位置的几何图形,是两条线相交处或线段的两端。数学公式确切地反映了事物内部和外部的关系。
...距离公式推荐访问