留学群专题频道等比数列前n项和栏目,提供与等比数列前n项和相关的所有资讯,希望我们所做的能让您感到满意!
11-15
等比数列是数学中一个重要的知识点,那么你知道等比数列的求和公式及其推导过程吗?下面是由留学群编辑为大家整理的“等比数列前n项和公式推导过程(实用)”,仅供参考,欢迎大家阅读本文。
等比数列前n项和公式
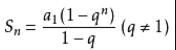
公式中a1为数列首项,q为等比数列的公比,Sn为前n项和。
等比数列前n项和公式推导过程
等比数列前n项和公式:Sn=a1(1-q^n)/(1-q)。
推导如下:
因为an=a1q^(n-1)
所以Sn=a1+a1*q^1+...+a1*q^(n-1)(1)
qSn=a1*q^1+a1q^2+...+a1*q^n(2)
(1)-(2)注意(1)式的第一项不变。
把(1)式的第二项减去(2)式的第一项。
把(1)式的第三项减去(2)式的第二项。
以此类推,把(1)式的第n项减去(2)式的第n-1项。
(2)式的第n项不变,这叫错位相减,其目的就是消去这此公共项。
于是得到
(1-q)Sn=a1(1-q^n)
即Sn=a1(1-q^n)/(1-q)。
拓展阅读:等比数列的性质
①在等比数列{an}{an}中,若m+n=p+q=2k(m,n,p,q,k∈N∗)m+n=p+q=2k(m,n,p,q,k∈N∗),则am⋅an=ap⋅aq=a2kam⋅an=ap⋅aq=ak2;
②若数列{an}{an},{bn}{bn}(项数相同)是等比数列,则{λan}(λ≠0){λan}(λ≠0),{1an}{1an},{a2n}{an2},{an⋅bn}{an⋅bn},{anbn}{anbn}仍然是等比数列;
③在等比数列{an}{an}中,等距离取出若干项也构成一个等比数列,即an,an+k,an+2k,an+3k,⋯an,an+k,an+2k,an+3k,⋯为等比数列,公比为qkqk;
④q≠1q≠1的等比数列的前2n2n项,S偶=a2⋅[1−(q2)n]1−q2S偶=a2⋅[1−(q2)n]1−q2,S奇=a1⋅[1−(q2)n]1−q2S奇=a1⋅[1−(q2)n]1−q2,则S偶S奇=qS偶S奇=q;
⑤等比数列的单调性,取决于两个参数a1a1和qq的取值,an=a1⋅qn−1an=a1⋅qn−1。
...
等比数列前n项和怎么算呢?公式又有哪些呢?同学们快来和小编一起看看吧。下面是由留学群小编为大家整理的“等比数列前n项和的公式”,仅供参考,欢迎大家阅读。
设数列{a×q^(n-1)}是首项为a,公比为q的等比数列。
即a, aq, aq², aq³, ^(n-1). (n=1,2,3,4...)
其前n项和为Sn,
当q=1时,Sn=na. (n=1,2,3,....)
当q≠1时,Sn=a[(q^n)-1]/(q-1) (n=1,2,3,...)。
等比数列前n项和公式推导
等比数列前n项和公式:Sn=a1(1-q^n)/(1-q)。
推导如下:
因为an=a1q^(n-1)
所以Sn=a1+a1*q^1+...+a1*q^(n-1)(1)
qSn=a1*q^1+a1q^2+...+a1*q^n(2)
(1)-(2)注意(1)式的第一项不变。
把(1)式的第二项减去(2)式的第一项。
把(1)式的第三项减去(2)式的第二项。
以此类推,把(1)式的第n项减去(2)式的第n-1项。
(2)式的第n项不变,这叫错位相减,其目的就是消去这此公共项。
于是得到
(1-q)Sn=a1(1-q^n)
即Sn=a1(1-q^n)/(1-q)。
1、若m、n、p、q∈N*,且m+n=p+q,则am*an=ap*aq;
2、在等比数列中,依次每k项之和仍成等比数列。“G是a、b的等比中项”“G^2=ab(G≠0)”;
3、若(an)是等比数列,公比为q1,(bn)也是等比数列,公比是q2,则(a2n),(a3n)…是等比数列,公比为q1^2,q1^3…(can),c是常数,(an*bn),(an/bn)是等比数列,公比为q1,q1q2,q1/q2;
4、按原来顺序抽取间隔相等的项,仍然是等比数列;
5、等比数列中,连续的,等长的,间隔相等的片段和为等比;
6、若(an)为等比数列且各项为正,公比为q,则(log以a为底an的对数)成等差,公差为log以a为底q的对数;
7、等比数列前n项之和Sn=A1(1-q^n)/(1-q)=A1(q^n-1)/(q-1)=(A1q^n)/(q-1)-A1/(q-1)(8)数列{An}是等比数列,An=pn+q,则An+K=pn+K也是等比数列,在等比数列中,首项A1与公比q都不为零.注意:上述公式中A^n表示A的n次方;
8、由于首项为a1,公比为q的等比数列的通向公式可以写成an*q/a1=q^n,它的指数函数y=a^x有着密切的联系,从而可以利用指数函数的性质来研究等比数列。
等比数列的有关概念
1、等比数列的定义:
一般地,如果一个数列从第二项起,每一项与它的前一项的比都等于一个常数(不为0),那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,公比通常用q来表示。<...
08-03
等比数列是高中数学重点知识之一,那么等比数列前n项和公式怎么求呢?下面是由留学群小编为大家整理的“等比数列前n项和公式怎么求”,仅供参考,欢迎大家阅读。
等比数列前n项和公式怎么求
等比数列前n项和公式:Sn=a1(1-q^n)/(1-q)。
推导如下:
因为an=a1q^(n-1)
所以Sn=a1+a1*q^1+...+a1*q^(n-1)(1)
qSn=a1*q^1+a1q^2+...+a1*q^n(2)
(1)-(2)注意(1)式的第一项不变。
把(1)式的第二项减去(2)式的第一项。
把(1)式的第三项减去(2)式的第二项。
以此类推,把(1)式的第n项减去(2)式的第n-1项。
(2)式的第n项不变,这叫错位相减,其目的就是消去这此公共项。
于是得到
(1-q)Sn=a1(1-q^n)
即Sn=a1(1-q^n)/(1-q)。
拓展阅读:等比数列的概念
(1)如果一个数列从第2项起,每一项与它的前一项的比等于同一个非零常数,那么这个数列叫做等比数列.
数学语言表达式:=q(n≥2,q为非零常数).
(2)如果三个数a,G,b成等比数列,那么G叫做a与b的等比中项,其中G=±。
2.等比数列的通项公式及前n项和公式
(1)若等比数列{an}的首项为a1,公比是q,则其通项公式为an=a1qn-1;
通项公式的推广:an=amqn-m.
(2)等比数列的前n项和公式:当q=1时,Sn=na1;当q≠1时,Sn==。
3.等比数列的性质
已知{an}是等比数列,Sn是数列{an}的前n项和.
(1)若k+l=m+n(k,l,m,n∈N*),则有ak·al=am·an。
(2)相隔等距离的项组成的数列仍是等比数列,即ak,
ak+m,ak+2m,…仍是等比数列,公比为qm。
(3)当q≠-1,或q=-1且n为奇数时,Sn,S2n-Sn,S3n-S2n,…仍成等比数列,其公比为qn。
...等比数列前n项和推荐访问